経 緯：
現在ロードバイク2台にそれぞれ CATEYE CC-TR300TW という同じサイクルコンピューターを搭載させていて、
タイヤの太さは1台目が26cで、2台目は32cを履いている。
たまに遠出するのだが、自宅から同じ経路で同じ場所を往復すると、遠ければ遠い程距離が一致しない。
どうも気持ちが悪いので、どうやったら距離の誤差を縮められるか？を検討してみた。
そんな事しなくても、スマートフォンのGPSで記録すればいいじゃないか! とも思うんだが、GPSそのものの
誤差もあるし、ビルの谷間を走行した後に経路記録を見ると、自分が数十メートル「瞬間移動」した事に
なっていたりで不満が大きい。
結局アナログ(?)なサイクルコンピューターの計測結果が一番だろう。
●今回の目標は誤差を 0.5% 以下にまで縮める事とする。
様々な方法：
サイクルコンピューターに設定すべき自分のタイヤ周長を知るには一般的(？)に以下の方法が考えられる。
●マニュアルに書かれている「参考目安」の「タイヤ周長ガイド」を利用する。
→
リムの太さやトレッドの高さなど、自分の環境と同じではないので、誤差が大きい。
あくまでも「目安」だった。
●マニュアル通りに、「タイヤの空気圧を適正にし、荷重をかけた状態で、バルブ等の目印になるものを基準に
してタイヤを1 回転させ、路面の寸法を測ります。」を実践してみる。
→
これは難しかった。メジャーを地面に置き、そのすぐ横で前後のタイヤに目印のテープを貼り、サドルを低く
して跨いで体重をとブレーキをかけながらてやってみたのだが、微妙によろけてしまい真直に自転車を移動
させるのに難儀した。数回トライして最も多く出た数値を採用した。
ちなみに、26cの場合は 2,112mm 、32cの場合は 2,130mm だった。
この方法だと2台の自転車の誤差はギリギリ許せる範囲だったが、実際の距離との誤差がイマイチ。
よく考えてみるとペダルを踏んだ時の横振れは考慮されないため、実際の距離とは誤差が出る筈だ。
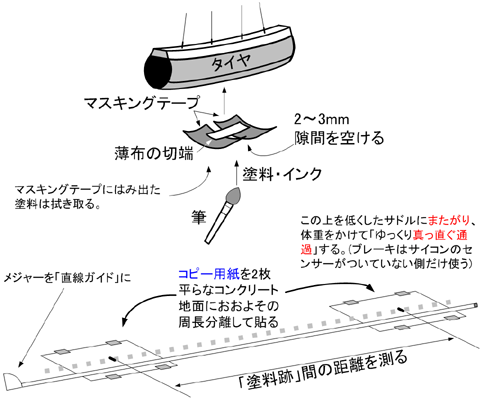
ちなみに、実際にはやらなかったが、下図の方法が「マニュアル通り」の最も正確な方法だろう。
●洋服の採寸などに使われるような柔らかく、且つ長いメジャーでタイヤ周長を直接測ってみる。
→
これはやらなかった。そのためだけに柔らかいメジャーを用意するのも何だし、体重負荷をかけた場合と値が
乖離しすぎる筈だし、次の方法の方が賢そうだ。
●タイヤの半径を正確に測り、2πrする。
→
これも実際にやってみた。地面が水平な場所で助手を自転車に跨がせ、体重をかけながら垂直に立せて、
スコヤ(又は三角定規でも)で垂直に立てた600mm定規を近づけて目を凝らしながら半径を測り計算した。
結果2台の誤差は0.1%と許せる範囲だったが、実際の距離との誤差が2%以上と「マニュアル通り」よりも悪化した。
また、この方法もペダリングによる横振れは考慮されない。
たどり着いた方法： ( 後日撤回 下記「後日談」を参照 )
河川の土手や国道に1km毎にある以下の様な「距離標」(キロポスト)を利用する。
設置は国交省の仕事だから正確なはずだ。多分。
長い距離から割り出すので測定の正確さが増すし、実走であればペダリングによる横振れも含める事ができる。
（ 本来なら 1km の間をタイヤが何周したのか？が判ればいいのだが、サイコンはわざわざ計算した結果(距離)
だけを表示し、センサーの単純なカウントは出してくれない。プログラムとしては簡単なんだが。。。 ）
その前にやってはいけない方法：
まず、「やってはいけないこと」なのだが、距離標の真横でサイクルコンピューターの距離を0mリセットして走行を
開始して、1km先の距離標の真横で停止する。(実際にやってみた)
この方法で同じ場所を数回往復したのだが、なぜか毎回数メートル距離が変わる。(サイクルコンピューターの単位は
10mなので、あくまでも感覚だが明らかに最大5m以上変わる)
多分サイクルコンピューターは停止状態だと判断する時間や、走行開始だと判断する時間があるからではなかろうか？
現に信号待ちの場合は走行時間のカウントも止まる仕様になってるし。
もう一つ「やってはいけないこと」なのだが、「距離標」の真横を通過する瞬間にサイクルコンピューターの距離を
0mリセットする事。これも毎回数メートル距離が変わってしまった。どうも通過する時のスピードによって変わるので、
同じ理由で走行開始と判断する時間のズレの問題と思われる。
以下が今回採用した方法：
(後日 撤回)
結局単純な方法だが、起点とする距離標の 100m 以上手前から走行を開始。起点を通過した瞬間の距離を覚えて
おいて、1km先の距離標を通過する瞬間の距離を見る。そのまま走行を続けて次の距離標でも同じ事をする。
信号待ちや、道路や橋の事情で河川の土手が蛇行してしまうような場所は避け、ノンストップでなるべく長く
真っ直ぐ走れる同じ所を同じ方法で往復する。(そういった意味でも河川のサイクリングコースが適している)
サイコンの距離単位は 10m だが、測定の数が多ければ多いほど、その傾向から 1m 単位の誤差まで推測で解る
ようになる。
上述の「タイヤの半径から2πrで求めた」26cのタイヤの周長 2,155mm の状態で今回の方法で誤差測定した場合。
距離標の 1,000m をサイクルコンピューターは 1,022m だと測定していると推測された。
つまり、2.2% 長い。2,155mm から 2.2% を引くと、
2155 ÷ 1.022 ≒ 2108.611
約 2,109mm という事になる。
32cの場合は 2,125mm だった。
それから数回走っているが、2台の自転車の誤差も実際の距離との誤差も 0.1% くらいに収まっている。
後日談：
その後、32c を履いたバイクのホイールとタイヤを新調した。
その際にサイコンの周長も新たに測り直す必要が出たため、上記の「マニュアル通りの最も正確な方法」を試してみた。
この方法での 32c のタイヤ(新たなホイール・タイヤの組合せ)の場合は、2,153mm だった。
そして、ついでに 26c のバイクもこの方法で測定してみた。(この 26c のバイクはホイールもタイヤも交換していない)
するとなんと！ 測定結果は 前回と同じ 2,108.6mm !!
数回繰り返しても結果は同じ。
前回は河川沿いの同じ場所を何度も何度も往復して、苦労して出した数値だったが、こんな簡単な方法でも同じ数値が出てしまった。
というわけで前回の「以下が今回採用した方法」は撤回。
マスキングテープ・薄布・塗料(インクでも) とコピー用紙2枚 の方法でＯＫ！！
